Convert EPUB file to PDF file

Convert EPUB file to PDF file

To convert any epub file to pdf format, there are many ways but the simplest on is shown here:

Using online service provided by 

http://ebook.online-convert.com/convert-to-pdf

Ruchi Singh, Educationist

Book on Function and Graphs

Function and Graphs

Book

I. M. Gelfand, E. G. Glagoleva, E. E. Shnol, "Functions and Graphs"
ISBN: 0486425649 | 2002 | EPUB | 112 pages | 7 MB

The second in a series of systematic studies by a celebrated mathematician I. M. Gelfand and colleagues, this volume presents students with a well-illustrated sequence of problems and exercises designed to illuminate the properties of functions and graphs. Since readers do not have the benefit of a blackboard on which a teacher constructs a graph, the authors abandoned the customary use of diagrams in which only the final form of the graph appears; instead, the book's margins feature step-by-step diagrams for the complete construction of each graph. 

The first part of the book employs simple functions to analyze the fundamental methods of constructing graphs. 

The second half deals with more complicated and refined questions concerning linear functions, quadratic trinomials, linear fractional functions, power functions, and rational functions.


Link

Ruchi Singh, Educationist

Fun with Functions

Some fun with Functions

Source : https://in.pinterest.com/source/buzzfeed.com/

Source : https://in.pinterest.com/pin/19794734610004950/

Ruchi Singh, Educationist

Function and Graph

This one of my favorite topic. And may be that the reason the first one in series of topics I had taken to share with you all !!!

Function  - for every x there is exactly one y. 

x ----->Operator --------> y

Here, x is the input. Function is like some operator, you can think of a machine and y as the output.

Now, 

x ----->Function --------> y

The values x can take is called DOMAIN

and the Y values can get is called RANGE.

Remember, for every x there is exactly one y, the first sentence of function definition.

Note that x and y are related to each other by this operator - Function.

Lets, take an example.

y = x^2 + 2

here, operator or function is x^2 + 2,

we can denote this function as f(x) = x^2 + 2

f(x) is called function of x, as it can take independent values to give values for f(x).

All the values x can take is its domain and all the values f(x) will get will range.

lets give some values to x,

x = -1  f(-1) = 1+2 = 3

x=0      f(0) = 0+2 = 2

x=1     f(1) = 1+2 = 3

x= 2    f(2) = 4+2 = 6

Also, note f(x) has unique value for each x. 



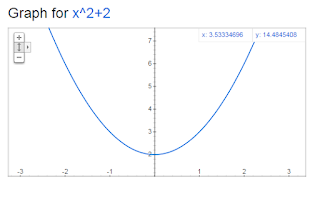
We took few values as input for the operator f(x) but x can take other values which can be

from   - infinity to + infinity.

Range will be as you can see from the graph 2 to + infinity.

Welcome to my blog – Mathsmania !

The blog is dedicated to all those learning basic maths. I will post series of introduction articles on Calculus, Trignometry, Algebra, Coordinate, Statics, Dynamics for Secondary class students.

Instructor : Ruchi Singh